Решение задачи 502

Условие:

Подсказка к задаче 502

Ноздрев имеет восемь чисел, прибавляя к которым или вычитая из которых ему надо получить число N.

Подсказка к задаче 500

Нарисуйте равносторонний треугольник и три полуокружности.

Решение задачи 500

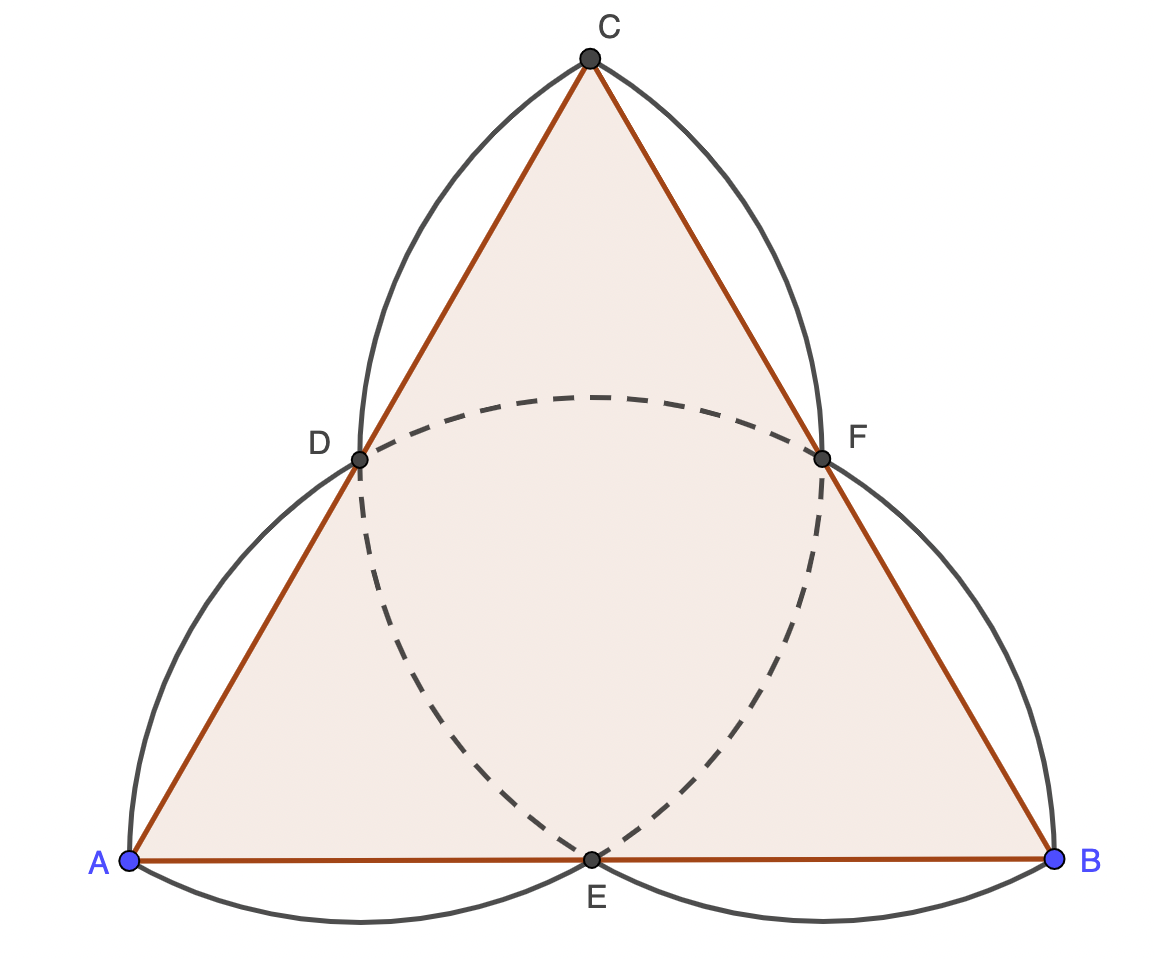
Условие: Существует ли такая отличная от круга фигура, ограниченная отрезками и дугами окружностей, что все отрезки, делящие пополам ее периметр, имеют одинаковые длины?

Подсказка к задаче 498

Переведите число p в двоичную дробь

Решение задачи 498

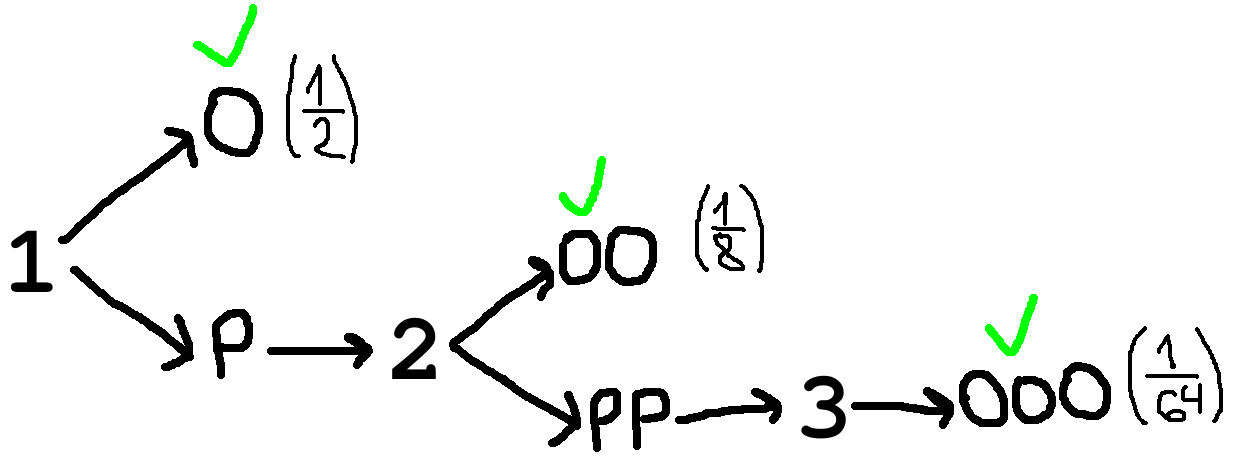
Дано вещественное число p из отрезка [0;1]. С помощью симметричной монетки реализовать вероятность p.

Подсказка к задаче 497

Изначально Лошадка может в одной из клеток, то есть 63 вариант. Переберите поочередено эти варианты.

Решение задачи 497

Условие:

Ответ на витражи

Подсказка к задаче 496

Поделите каждый член прогрессии на минимальную степень p^n q^m, где n и m минимальные степени вхождения p и q среди членов прогрессии.