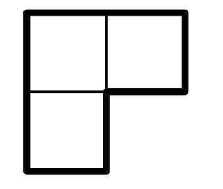
Подсказка к задаче 435
Рассмотрите две верхние строки. Может ли в разбиении быть уголок, который пересекается второй строкой, но не пересекается певой?
53
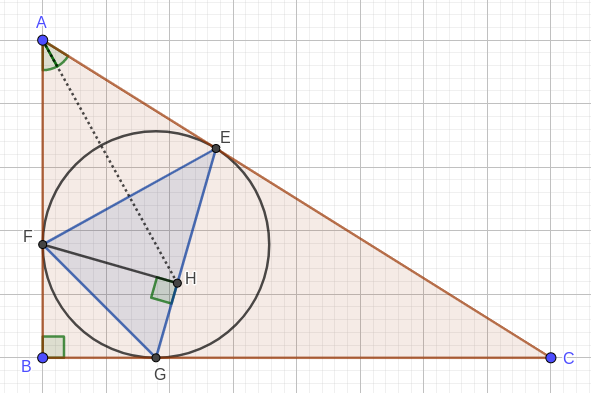
Подсказка к задаче 434
Пусть I — центр вписанной окружности треугольника ABC. Попытайтесь доказать, что точки A, I, H лежат на одной прямой.
70
Подсказка к задаче 427
Рассмотрите три числа, которые находятся в одном десятке. Могут ли все суммы их цифр быть простыми?
64
Нет трех подряд идущих простых чисел!
Посмотрим на эти три числа с точки зрения их четности. Возможны два варианта (Ч — четное, Н — нечетное) : ЧНЧ, НЧН.
93
Подсказка к задаче 423
Попытайтесь доказать, что x и y обязаны быть четными числами, после чего сделайте замену x = 2x₁, y = 2y₁.
191